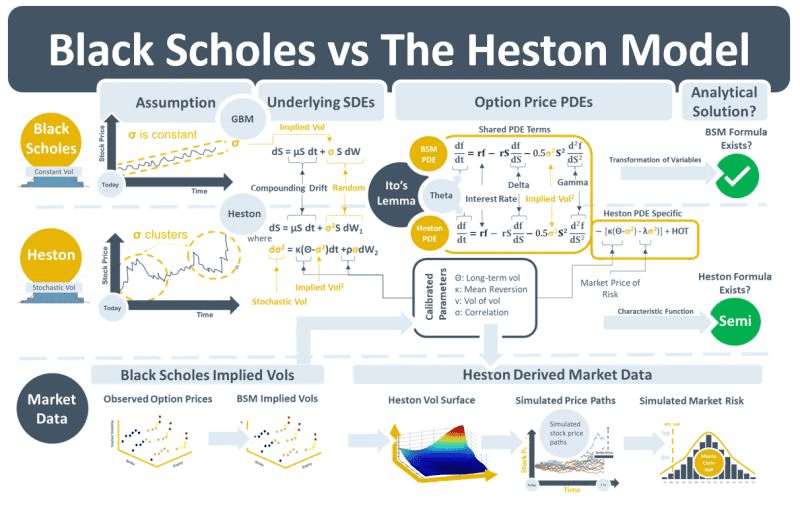
On market data projects, implied volatilities are loaded from brokers and data vendors and need to be validated. Often, they also need to be compared to internally calculated volatilities for IPV and other purposes. This week’s note discusses the difference between two quantitative models, Black Scholes and the Heston model, and their different assumptions and approaches to modelling volatility.
Geometric Brownian motion (GBM) models stock prices as having a growth rate that compounds over time plus a random component. GBM is the stochastic differential equation (SDE) that underlies the Black Scholes Merton (BSM) model. GBM is converted into the BSM partial differential equation (PDE) for option price movements using Ito’s Lemma.
The SDE that underlies the Heston model is similar to GBM but the random component assumes that volatility can vary over time. As with the BSM model, the Heston SDE is converted into the Heston option price PDE using Ito’s Lemma.
The BSM option price PDE and the Heston PDE have shared terms. Both assume that the change in the option price over time (df/dt) is dependent on the interaction between an interest rate term (rf), a delta term (df/dS), and a second order (gamma) term. The coefficient of the gamma term includes implied vol (σ). The Heston PDE, however, has additional terms that are not contained in the BSM PDE. These additional terms primarily relate to the behaviour of vol and they contain the Heston model parameters. The parameters include long-term vol, the rate of mean-reversion, the volatility of the vol, and the correlation between the vol movement and the underlying stock price movement. Closed form solutions (formulas) exist for both the BSM and Heston PDEs.
Option prices can easily be converted into BSM implied vols (IVs). Broadly, the option prices and IVs can be considered observable market prices. The Heston model parameters are calibrated so that they generate a continuous Heston volatility surface that fits the observable data. Once the Heston parameters and the Heston vols are generated then they can be used to simulate price paths for valuing different types of derivatives. The parameters can also be used for simulating price paths for use in market risk models.